Welcome to SORA Project


Thank you so much for your continued support of SORA since 2018. On this website, SORA SorachanCoin L1 cryptographic keys and mining Quantum-resistance, we continue our research into cryptographic keys with quantum resistance. Due to the fact that quantum-related issues affect both ECDSA and Proof of Work (PoW), resolving them is expected to take considerable time.
As such, we are shifting our focus toward SORA L2 Blockchain FromHDDtoSSD, which utilizes 2048-bit quantum-resistant keys and allows for greater flexibility in operation. SORA L2 features decentralized HDD/SSD/NVMe drive inspection, data recovery functionality, and AI-NFT support. By leveraging AI-NFT, we enable decentralized AI processing on the blockchain, delivered as Windows-based software. Naturally, SORA L2 operates as a full node as well.
Let’s get started simply download and run the program. It supports Windows 11, 10, 8.1, 8, and 7.
Download:SORA L2 Blockchain FromHDDtoSSD
On Quantum Computers and Probability Amplitudes
In the example above, we were able to significantly increase the probability amplitude for maintaining the frequency domain. However, such cases are rare, and quantum computers are weak at tasks like finding the preimage of a hash designed to lack periodicity. This is because, without periodicity, there is no effective method to significantly increase the probability amplitude of the value to be observed.
While there are methods to gradually increase the probability amplitude, they only scale by approximately the square root and are therefore impractical. Consequently, by incorporating mathematical elements that make it difficult to enhance probability amplitudes into the signatures of public-key cryptographic systems, it is possible to achieve quantum resistance for blockchain systems.
The following image represents the quantum resistance integrated into SORA L1. It incorporates signatures that utilize this property.
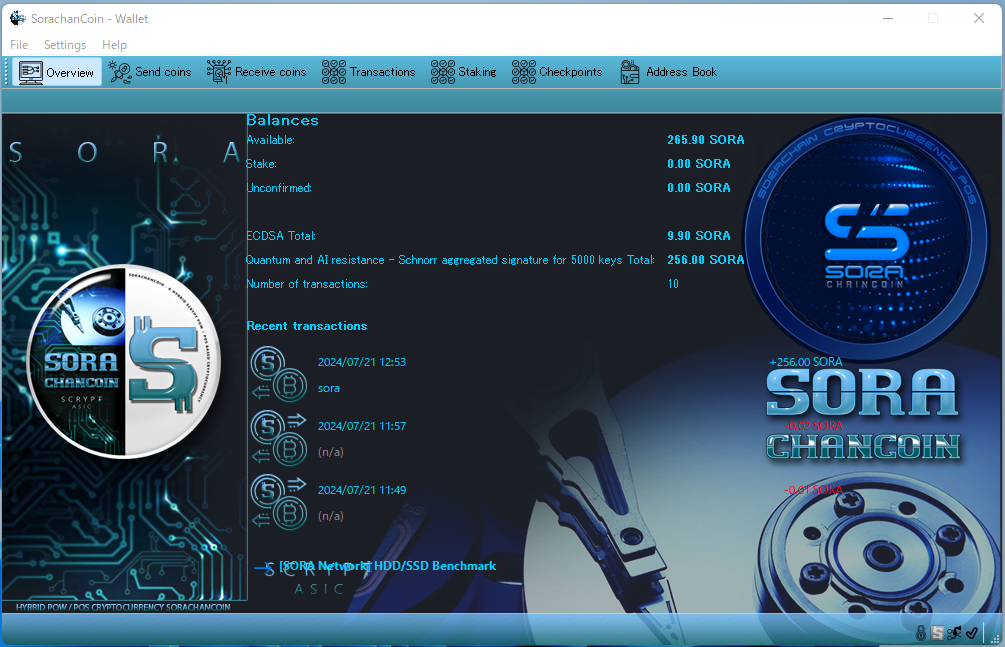
Balances separated between ECDSA and Quantum resistance
The SORA Quantum-Resistant Blockchain automatically separates the balances of the widely adopted ECDSA cryptography, used in Bitcoin and similar systems, and the quantum-resistant cryptography uniquely enhanced and implemented by SORA. Users can utilize both ECDSA and quantum-resistant cryptography without being aware of the differences. Specialized knowledge, such as multisig, is "not required." Simply using the blockchain as usual allows you to enjoy the benefits of quantum resistance.
AI-NFT
Support for ownership management, metaverse, drive(HDD/SSD/NVMe) inspection and advanced scientific analysis ... etc.
Web3 - Blockchain - Multidimensional NFT by SORA Network. We aim to popularize multidimensional NFTs that can be built by direct product based on Web3 - blockchain technology. The base development has already been completed, and 1-dim NFT, 2-dim NFT, and 4-dim NFT are operating normally on SORA Network.

SORA L1 Quantum Resistance in Blockchain Core

We have implemented quantum resistance directly on L1, eliminating the need for a bridge.
The traditional public-key cryptography method, ECDSA, widely used in Bitcoin and other systems, uses addresses that start with "S." In contrast, quantum-resistant transactions incorporating SORA's proprietary quantum-resistant signature use addresses that start with "sora1."
The implementation is remarkably simple!
SORA L2 Quantum Resistance in Blockchain AI-NFT
On SORA L2, we are developing blockchain-based applications. Please feel free to make use of them as well. In the following image, blockchain is integrated with other functionalities, operating inspection features and more with AI in the background.

About the Specifications

| Maximum issuance amount | 8,000,000 |
| Current circulating supply | https://us.junkhdd.com:7350/ext/getmoneysupply |
| Block explorer | https://us.junkhdd.com:7350/ |
| Block generation time | 3 minutes |
| Hashing algorithm | Scrypt |
| Consensus | PoW + PoS Hybrid |
| PoW reward | 1 SORA / block |
| PoS reward | 3% / year |
| CoinMarketCap | https://coinmarketcap.com/currencies/sorachancoin/ |
| CoinCodex | https://coincodex.com/crypto/sorachancoin/ |
| CoinGecko | https://www.coingecko.com/en/coins/sorachancoin |
| CryptoSky | https://discord.gg/bAEgA8sczE |